Assistant Professor Abigail Raz Co-Authors Paper Published in Discrete Applied Mathematics
POSTED ON: May 24, 2024
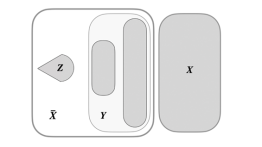
Figure 1 from the paper: The subsets X, X̄, Y, and Z as define within the IIM graph H.
Assistant Professor of Mathematics Abigail Raz has been co-published in Discrete Applied Mathematics (Volume 341, December 2023). Coauthored by Professor Raz and Assistant Professor Erin Meger from Queens University, Kingston, Canada, the paper is titled “The Iterative Independent Model.”
To read more about the publication, please click here.
ABSTRACT
Deterministic complex networks that use iterative generation algorithms have been found to more closely mirror properties found in real world networks than the traditional uniform random graph models. In this paper we introduce a new, Iterative Independent Model (IIM), generalizing previously defined models in Bonato et al. (2020, 2009, 2017). These models use ideas from Structural Balance Theory to generate edges through a notion of cloning where “the friend of my friend is my friend” and anticloning where “the enemy of my enemy is my friend” (Bonato et al., 2020; Easley et al., 2010). In this paper, we vastly generalize these notions by allowing each vertex added at a given time step to choose independently of the other vertices if it will be cloned or anticloned. While it may seem natural to focus on a randomized model, where we randomly determine whether or not to clone any given vertex, we found the general deterministic model exhibited certain structural properties regardless of the probabilities. This allows applications to then explore the particulars, while having the theoretical model explain the structural phenomenons that occur in all possible scenarios.
Throughout the paper we demonstrate that all IIM graphs have spectral gap bounded away from zero, which indicates the clustering properties also found in social networks. Furthermore, we show bounds on the diameter, domination number, and clique number further indicating the well clustered behavior of IIM graphs. Finally, for any fixed graph F
all IIM graphs will eventually contain an induced copy of F.




